1.Röntgendiffraktometer

WennRöntgenbeugung Wird als elektromagnetische Welle in einen Kristall projiziert, wird sie von den Atomen im Kristall gestreut, und die gestreuten Wellen scheinen vom Zentrum der Atome auszugehen, und die vom Zentrum jedes Atoms emittierten gestreuten Wellen ähneln der Quelle Kugelwellen. Da die Atome im Kristall periodisch angeordnet sind, besteht zwischen diesen gestreuten Kugelwellen eine feste Phasenbeziehung, die dazu führt, dass sich die Kugelwellen in einigen Streurichtungen gegenseitig verstärken und in einigen Richtungen gegenseitig aufheben, was zu Beugungsphänomenen führt.

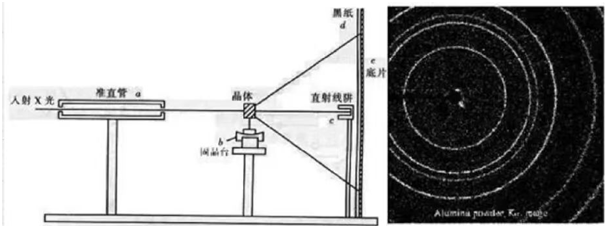
2. Bragg-Gleichung – der theoretische Eckpfeiler vonXRD

2dsin0=n in (wobei day der Einfallswinkel, d der Abstand zwischen den Kristallflächen, n die Beugungsordnung, in die Wellenlänge des einfallenden Strahls und 20 der Beugungswinkel ist)

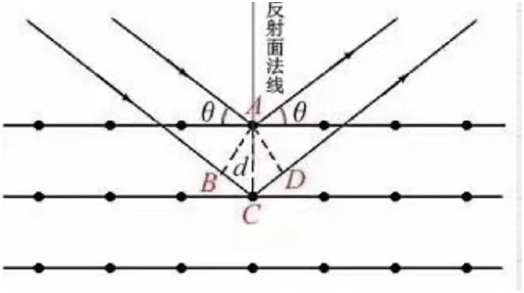
Die Bragg-Gleichung ist die Grundbedingung dafürRöntgenbeugungin einem Kristall und spiegelt die Beziehung zwischen der Richtung der Beugungslinie und der Kristallstruktur wider.

Aufmerksamkeit:

(a) Alle atomaren Beugungswellenphasen auf allen Kristallebenen in allen Richtungen, die die Bragg-Gleichung erfüllen, sind genau gleich und ihre Amplituden verstärken sich gegenseitig. Auf diese Weise erscheinen Beugungslinien oberhalb der 20-Richtung und heben sich an anderer Stelle gegenseitig auf, und die Intensität der Röntgenstrahlung wird verringert oder gleich Null.

(b) Der Reflexionswinkel vonRöntgenstrahlenunterscheidet sich von dem des sichtbaren Lichts und der Winkel zwischen dem Einfallswinkel und dem Reflexionswinkel von Röntgenstrahlen beträgt immer 20.

3. Scherrer-Formel – die theoretische Grundlage der Korngrößenmessung

Die Breite desRöntgenbeugungDas Band hängt von der Korngröße ab. Je kleiner das Korn ist, desto diffuser und breiter wird die Beugungslinie. Sie ist auch als Scherrer-Formel bekannt und beschreibt die Beziehung zwischen der Korngröße und der Halbwertsbreite des Beugungspeaks.

K ist die Cherrer-Konstante, B ist die Halbwertsbreite und Höhe des Beugungspeaks, K=0,89, wenn B die Integralbreite des Beugungspeaks ist, K=1

ichist der Beugungswinkel, λ ist die Röntgenwellenlänge und d ist die durchschnittliche Dicke senkrecht zur Kristallfläche.

Aufmerksamkeit:

Die Verwendung dieser Gleichung zur Berechnung der durchschnittlichen Partikelgröße erfordert Aufmerksamkeit:

(1) ist die Halbwertsbreite, also die Breite, bei der die Beugungsintensität die Hälfte des Maximalwerts beträgt, und die Einheit ist das Bogenmaß.

(2) Messbereich 3-200 nm.